I❤️LA: Compilable Markdown for Linear Algebra

Yong Li, Shoaib Kamil, Alec Jacobson, Yotam Gingold

In-Browser Compiler (Chrome or Firefox, not Safari)

Language Reference

Discord

Code: GitHub

Paper: Transactions on Graphics (SIGGRAPH Asia 2021) [PDF 9 MB]

Examples from the Wild

Integrating with Existing Code

Follow-up work: H❤️rtDown: Document Processor for Executable Linear Algebra Papers

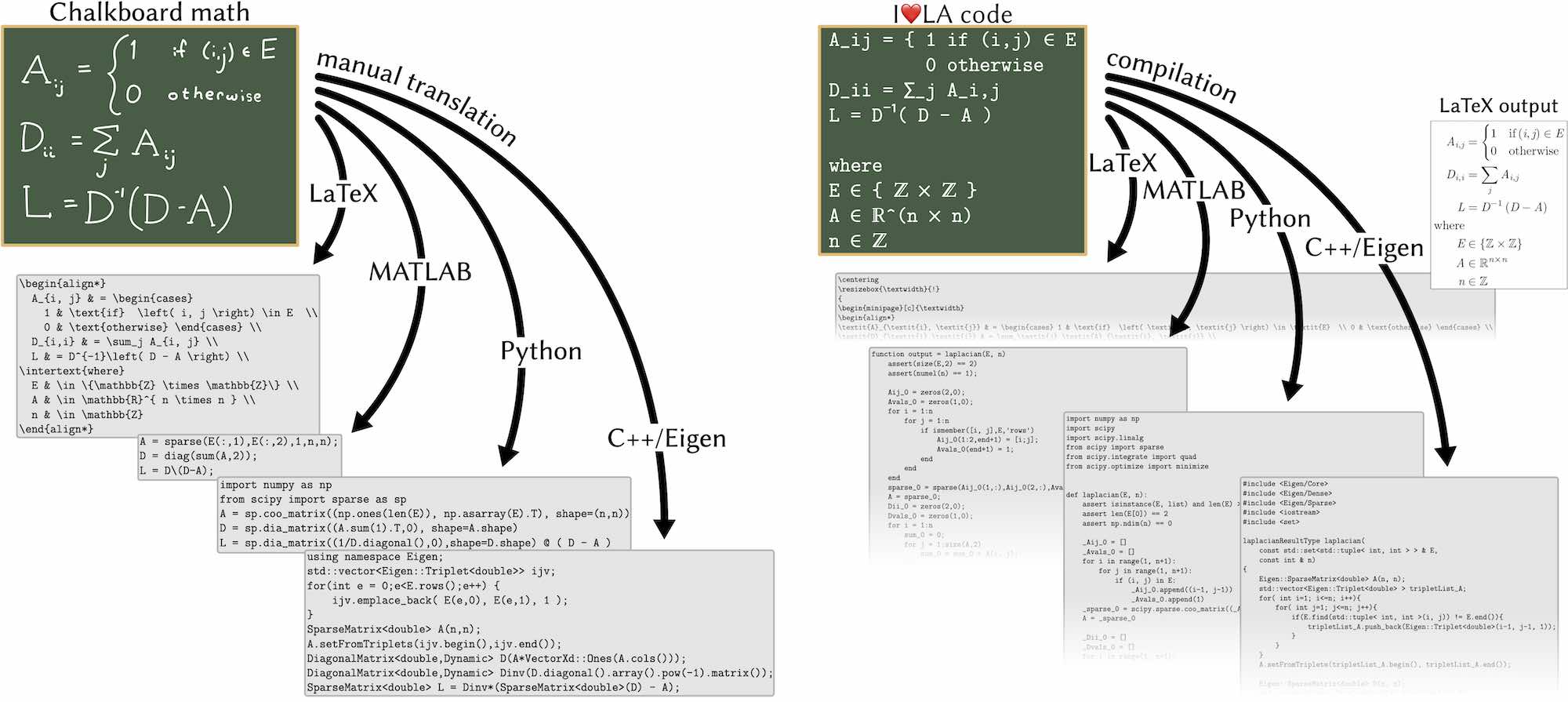
Mathematical notation has evolved over centuries to efficiently communicate technical concepts such as the sparse graph Laplacian construction in the top left. Meanwhile, programming languages communicate with a machine typically with a reduced character set and syntax causing handwritten translation of mathematics to visually stray far from the “chalkboard math” and from each other.
I❤️LA is a novel domain specific language for linear algebra. The I❤️LA code written with rich Unicode symbols visually resembles chalkboard math, while still being a semantically well-defined programming language compilable to various target languages: LaTeX, MATLAB, Python, C++.

Abstract:

Communicating linear algebra in written form is challenging: mathematicians must choose between writing in languages that produce well-formatted but semantically-underdefined representations such as LaTeX; or languages with well-defined semantics but notation unlike conventional math, such as C++/Eigen. In both cases, the underlying linear algebra is obfuscated by the requirements of esoteric language syntax (as in LaTeX) or awkward APIs due to language semantics (as in C++). The gap between representations results in communication challenges, including underspecified and irreproducible research results, difficulty teaching math concepts underlying complex numerical code, as well as repeated, redundant, and error-prone translations from communicated linear algebra to executable code. We introduce I❤️LA, a language with syntax designed to closely mimic conventionally-written linear algebra, while still ensuring an unambiguous, compilable interpretation. Inspired by Markdown, a language for writing naturally-structured plain text files that translate into valid HTML, I❤️LA allows users to write linear algebra in text form and compile the same source into LaTeX, C++/Eigen, Python/NumPy/SciPy, and MATLAB, with easy extension to further math programming environments. We outline the principles of our language design and highlight design decisions that balance between readability and precise semantics, and demonstrate through case studies the ability for I❤️LA to bridge the semantic gap between conventionally-written linear algebra and unambiguous interpretation in math programming environments.

Fast Forward [SIGGRAPH Asia 2021]

Download as: MP4 [27 MB]

5-minute Presentation [SIGGRAPH Asia 2021]

Download as: MP4 [30 MB]

20-minute Presentation [SIGGRAPH Asia 2021]

Download as: MP4 [60 MB] | Keynote [250 MB] | PDF [60 MB] | PDF with notes [20 MB]

BibTeX (approximate):

@article{li2021iheartla,
 author    = {Li, Yong and Kamil, Shoaib and Jacobson, Alec and Gingold, Yotam},
 title     = {I Heart LA: Compilable Markdown for Linear Algebra},
 journal   = {ACM Transactions on Graphics (TOG)},
 volume    = {40},
 number    = {6},
 year      = {2021},
 month     = dec,
 keywords  = {linear algebra, mathematical input, domain-specific language, compiler, scientific computing}
}